Penyederhanaan Fungsi Boolean Dengan Karnaugh Map

PENYEDERHANAAN DUA VARIABEL

Contoh 1.

F = AB + A'B + AB'

Penyelesaian:

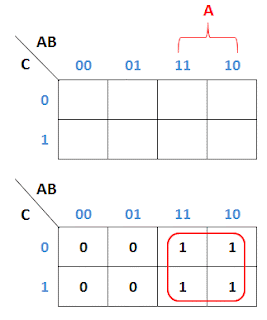
1.    Gambarkan K-Map Model-1 untuk dua variable

2.    Ganti kotak-kotak yang sesuai untuk AB, A'B, dan AB, dengan angka satu (1) dan sisanya dengan angka nol (0)

3.    Gabungkan semua angka satu (1) sesederhana mungkin. Untuk mempermudah dapat menggunakan pemetaan K-Map dua variabel.

4.    Hasil penyederhanaan dari F = AB + A'B + AB' adalah

                                                       F = A + B

Perbandingan dengan cara Aljabar:

F = AB + A'B + AB'

   = A (B+B') + A'B

   = A (1) + A'B

   = A + A'B

   = A + B

Contoh 2.

F = AB' + A'B'

Penyelesaian:

1.    Gambarkan K-Map Model-1 untuk dua variable

2.    Ganti kotak-kotak yang sesuai untuk AB' dan A'B' dengan angka satu (1) dan sisanya dengan angka nol (0)

3.    Gabungkan semua angka satu (1) sesederhana mungkin. Untuk mempermudah dapat menggunakan pemetaan K-Map dua variabel.

4.    Hasil penyederhanaan adalah F = B'

Perbandingan dengan cara Aljabar:

F = AB' + A'B'  

   = (A+A') B'

   = (1) B'

    = B'

PENYEDERHANAAN TIGA VARIABEL

Contoh 1.

F = ABC' + AB'C' + AB'C + ABC

Penyelesaian:

1.    Gambarkan K-Map Model-1 untuk 3 variabel kemudian tandai dengan angka satu (1) setiap kotak yang mewakili ABC', AB'C', AB'C, dan ABC, sisanya diisi dengan angka nol (0).

2.    Gambarkan pemetaan K-Map untuk 3 variabel yang paling mendekati dan paling sederhana. Pada kasus ini area A pada K-Map dapat mewakili semua variabel dalam soal.

3.    Hasil penyederhanaan dari F = ABC' + AB'C' + AB'C + ABC adalah

                                                       F = A

Perbandingan dengan Aljabar:

F = ABC' + AB'C' + AB'C + ABC

   = AB (C'+C) + AB' (C'+C)

   = AB (1) + AB' (1)

   = AB + AB'

   = A (B+B')

   = A (1)

    = A

Contoh 2.

F = A'B'C + A'BC + AB'C + ABC + ABC'

Penyelesaian

1.    Gambarkan K-Map Model-1 untuk 3 variabel kemudian tandai dengan angka satu (1) setiap kotak yang mewakili A'B'C, A'BC, AB'C, dan ABC, dan ABC', sisanya diisi dengan angka nol (0).

2.    Gambarkan pemetaan K-Map untuk 3 variabel yang paling mendekati dan paling sederhana. Pada kasus ini area AB dan area C pada K-Map dapat mewakili semua variabel dalam soal.

3.    Penyederhanaan dari F = A'B'C + A'BC + AB'C + ABC + ABC' adalah

                                              F = AB + C

Perbandingan dengan Aljabar:

F = A'B'C + A'BC + AB'C + ABC + ABC'

    = (A'+A)B'C + (A'+A)BC + ABC'

    = (1) B'C + (1) BC + ABC'

    = B'C + BC + ABC'

    = (B'+B)C + ABC'

    = (1) C + ABC'

    = C + ABC'

    = C + AB

    = AB + C

PENYEDERHANAAN EMPAT VARIABEL

Contoh

F = A'BC'D + ABC'D + A'BCD + ABCD

Penyelesaian

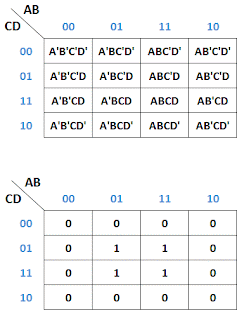
1.    Gambarkan K-Map Model-1 untuk 4 variabel kemudian tandai dengan angka satu (1) setiap kotak yang mewakili A'BC'D, ABC'D, A'BCD, ABCD, sisanya diisi dengan angka nol (0).

2.    Gambarkan pemetaan K-Map untuk 4 variabel yang paling mendekati dan paling sederhana. Pada kasus ini area B dab D pada K-Map dapat mewakili semua variabel dalam soal.

3.    Hasil penyederhanaan dari F = A'BC'D + ABC'D + A'BCD + ABCD adalah

                                                       F = BD

Perbandingan dengan Aljabar:

F = A'BC'D + ABC'D + A'BCD + ABCD

   = (A'+A) BC'D + (A'+A) BCD

   = (1) BC'D + (1) BCD

   = BC'D + BCD

   = BD (C'+C)

   = BD (1)

    = BD

Referensi :

http://www.linksukses.com/2012/11/logika-boolean-karnaugh-map.html